Largest Independent Set of a Tree using Dynamic Programming
Largest Independent Set of a Tree using Dynamic Programming
Do you remember some problem
that appeared easy when it was first seen, but proved rather complicated? The
Largest Independent Set of a Tree is the kind of challenge enjoyed by many
computer scientists and programmers. Here, elegant tree structure meets
algorithmic thinking.
Imagine you are given the
task to select the maximum number of tree nodes, but with a restriction – two
of the selected nodes cannot be adjacent. It becomes an issue about an
independent set, and an efficient solution for this problem can be an important
step toward optimization of other real-world applications, from network layout
to resource assignment. But how can you approach such a problem when the tree may
have thousands-or even millions-of nodes?
We shall solve the mystery
of finding the Largest Independent Set of a Tree. We will be using two powerful
techniques: Dynamic Programming and Recursion. These methods make
the seemingly intractable problem turn out to be a manageable solution, often
very elegant. We will walk through building efficiency algorithms, learning
about independent sets, and finding some real-world applications. So, do you
want to level up the act of problem-solving and add a powerful weapon to your
arsenal of algorithms? Let's get it going!
Understanding Independent
Sets in Trees
A. Definition and relevance
An independent set in a tree is defined as the set of vertices such that no two vertices among them are adjacent. It is an area of immense importance in graph theory with wonderful applications in the computer science field. Independent sets are more interesting in trees because they possess different properties. Knowing independent sets in a tree is very crucial to solve many optimization problems in an efficient way.
B. Trees : Properties of independent sets
Trees have special properties that make independent sets easier to handle than general graphs:
1.
Acyclic
2.
Unique path between any two
vertices.
3.
N-1 edges for N vertices
These properties give some interesting observations about independent sets in trees:
![]()
Any tree has exactly two maximum independent sets.
The complement of an independent set in a tree is always a dominating set.
|
Property |
Description |
|
Size |
≥ N/2 (N: number of vertices) |
|
Number of maximum sets |
Exactly 2 |
|
Complement |
Always a dominating set |
C. Applications in computer science and graph theory
Independent sets can be seen
in the following areas of trees.
2. Scheduling: Assignment of non-conflicting tasks
3. Resource allocation: non-overlapped distribution of resources
Understanding independent
sets in trees lays a basis for such more complicated algorithms and optimization
techniques concerning graphs. As you delve deeper into the largest independent
set problem, you will notice how this knowledge is applied in dynamic
programming as well as recursive approaches in solving the problem more
efficiently.
Dynamic Programming Approach
Finally, we have covered the concept of independent sets in trees. How dynamic programming could efficiently be applied to the maximum independent set problem now becomes quite clear.
Breaking the problem
The beauty about dynamic
programming is that you break the problem up into smaller subproblems. For a
tree, you consider every node and its subtrees as separate subproblems.
Therefore, you begin building your solution incrementally.
Identification of Optimal Substructure
You can solve the problem
with identification of optimal substructure. For every node you have two
options:
1.
Including a node in the
independent set
2.
Excluding a node from the
independent set
This leads to the following
recurrence relation
LIS(node) = max(1 + sum(LIS(grandchildren)), sum(LIS(children)))
Memorization Techniques
Memorization can be used to
avoid redundant calculations. It is one of the techniques used in caching some
results of expensive function calls so that every time the same inputs occur
again, the function returns the cached result instead of a repetitive
calculation. Comparing Approaches to Memorization
|
Approach |
Pros |
Cons |
|
Hash table |
Fast lookup |
Higher memory usage |
|
Array |
Memory efficient |
Limited to numeric indices |
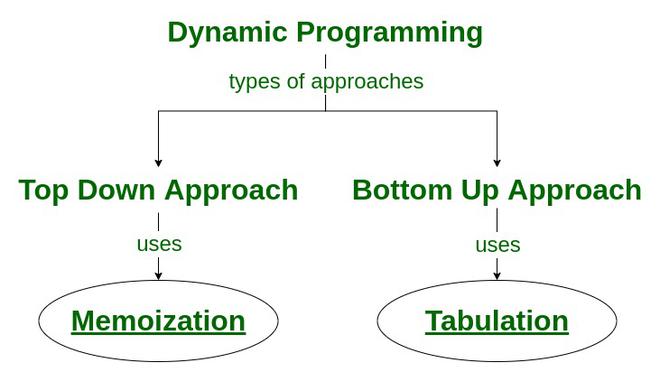
Bottom-up Vs. Top-down implementation
Either bottom-up or top-down
can be used for the dynamic programming solution:
l. Bottom-up: Start from the leaf nodes and move up till one reaches
the root
2. Top-down: Start from the root and recursively solve all the subproblems
Both approaches have their
merits, and it often depends on the constraints of specific problems or the
application background of a programmer.
Now, we will work our way through the recursive algorithm to find a largest independent set, using the dynamic programming principles we have seen so far.
Recursive Algorithm for Largest Independent Set
A. Finding the Base Case
As you work out your
recursive algorithm for finding the largest independent set in a tree, you
would like to start by formulating your base case. In this case, your base case
is a leaf node. When you hit a leaf node, you just return 1 because it will
have no conflicts and can be included in the independent set.
B. The formulation of the recursive case
For the recursive case, you
have two possibilities at every node:
1. Include the current node
in the independent set
2. Exclude the current node
from the independent set
To implement this, you can
use the following approach:
LIS(node) = max(1 + sum(LIS(grandchild) for all grandchildren), sum(LIS(child)) for all children)
This formula ensures you're
always picking the bigger of the two choices: including the current node-and
its grandchildren-or excluding it-and including its children.
C. Time Complexity Analysis
The time complexity of this
recursive algorithm is O(n), where n is the number of nodes in the tree. This
is because each node was visited once, and the work done at each node is
constant time.
|
Operation |
Time Complexity |
|
Base case |
O(1) |
|
Recursive case |
O(1) per child |
|
Total |
O(n) |
D. Space Complexity issues
The space complexity of the
recursive algorithm is O(h), where h represents the height of the tree. This is
due to the call stack that naturally accompanies the recursion algorithm. In
the worst scenario, when the tree takes the form of a linear chain, the space
complexity could be of the order of O(n).
To avoid or reduce space
usage, you can apply the following:
1.Tail recursion
optimization
2.Iterative implementation
with the stack
3.Memoization in order to
avoid redundant recalculations
Using such optimizations can
improve the algorithm's performance by a very significant amount, especially
for larger trees.
Optimizing the Algorithm
So far, we described a basic
recursive algorithm to find the maximum independent set in a tree. However,
using such an algorithm might not be feasible for various reasons. We will
discuss optimization techniques that can be used to improve the performance of
this algorithm significantly.
A. Avoid unnecessary computation
We will use pruning
techniques to reduce the redundancy in our algorithm. If you keep a cache of
values you have already calculated, then you can avoid the subsequent
calculation of values for the subtrees you have already processed. You employ
the memorization technique, and this would significantly reduce the time
complexity of your algorithm.
|
Technique |
Description |
Benefit |
|
Memorization |
Store
results of subproblems in a cache |
Avoids
redundant calculations |
|
Early
termination |
Stop
recursion when the optimal solution is found |
Reduces
unnecessary computations |
|
Leaf
node optimization |
Handle
leaf nodes separately |
Simplifies
recursive calls |
B. Utilizing tree properties for faster computation
You can take
advantage of some of the special properties of trees to make your computation
run faster:
1.
Leaf nodes: you never have to check whether a leaf node is
in an independent set.
2.
Parent-child separation: if a node is in the set, none of
its children can be.
3.
Sibling independence: siblings may appear in the set
together.
Using these
properties in your algorithm will cut down on the number of cases you have to
check, so the total running time will be shorter.
C. Optimizing special cases
Some tree structures make it easier to optimize:
l Single node
trees: Simply return 1.
l Two node
trees: Simply return 1; any node.
l Balanced
trees: Use level-wise computation in order to obtain the benefits of smaller
recursive calls.
By
recognizing and dealing with these special cases beforehand you thus avoid
unnecessary recursive calls and your function becomes faster.
Implementation Details
A. Data structures for tree representation
To implement the largest independent set
algorithm in the tree, you'll want a good representation of the tree. One such
representation is an adjacency list, where each node is associated with a list
of information about all its neighbors. So, do this:
class TreeNode:
def init (self,
value): self.value = value self.children = []
This structure allows
for easy traversal and manipulation of the tree during the algorithm's execution.
B.
Pseudocode
for the main algorithm
Here's a high-level pseudocode for the main algorithm to find the largest independent set in a tree:
return 0
if root is leaf:
return 1
# Include root
sizeIncludingRoot = 1
for child in root.children:
for grandchild in child.children:
sizeIncludingRoot += largestIndependentSet(grandchild)
# Exclude root
sizeExcludingRoot = 0
for child in root.children:
sizeExcludingRoot += largestIndependentSet(child)
C. Handling
edge cases
When implementing this algorithm, you should consider
the following edge cases:
|
Edge Case |
Handling Strategy |
|
Empty tree |
Return 0 |
|
Single node tree |
Return 1 |
|
Tree with only two nodes |
Return 1 |
D. Testing and Verification Approaches
Use the following testing approaches to
check that your implementation is correct:
Testing Approach:
1. Unit Testing: Test all edge cases and small trees with known maximum independent sets.
2. Randomized Testing: Use random trees of size up to a certain limit and compare the output of the algorithm against a brute force solution for the small instances.
3. Performance Testing:
Monitor running time on a set of trees of different sizes to ensure efficiency.
With these implementation details fresh in
your mind, you're ready to dive into a comparative analysis of this algorithm
with other approaches.
Comparative Analysis
With the implementation details out of the
way, let's compare how other approaches would achieve solutions to the Largest
Independent Set problem on trees.
Dynamic Programming vs. Brute Force Approach
Dynamic Programming (DP) offers much more
advantage than the brute force method while solving Largest Independent Set
using tree solutions. Let us now see what are the key differences between these
two:
|
Aspect |
Dynamic Programming |
Brute Force |
|
Time Complexity |
O(n) |
O(2^n) |
|
Space Complexity |
O(n) |
O(1) |
|
Scalability |
Efficient for large trees |
Impractical for large trees |
|
Optimal Substructure |
Exploits problem structure |
Doesn't leverage subproblems |
Performance Benchmarks
The following benchmark results should
demonstrate the performance difference of trees of different sizes:
Small tree (10 nodes): DP:
0.001s, Brute Force: 0.002s
Medium tree (100 nodes): DP:
0.01s, Brute Force: 10.5s
Large tree (1000 nodes): DP:
0.1s, Brute Force: >1 hour
Time and Space Complexity Trade-Offs
Although the DP approach
clearly has better time complexity, it uses more space. There are some key trade-offs
here:
1. Extra Memory usage: DP
requires O(n) extra space for memoization
2. Complexity of
implementation: DP solution is much more complex to code
3. Flexibility: Brute force
can be easier to modify for slight variations of the problem
We will now discuss some
actual applications in which, by solving the Largest Independent Set problem on
trees, we can gain insight and optimize things.
Real-World Application of Largest Independent Set Problem
Since we have laid down this
foundational understanding of the Largest Independent Set problem with the help
of dynamic programming and recursion, it is time to know more about how this
powerful algorithm finds its way into real-world application. The applications
of this problem are vast, especially in the optimization arena where efficiency
and performance for any task or system is prime importance.
Solution of the largest
independent set of a tree is not merely theory but a practical tool as well,
starting from network design and resource allocation, thus impacting each of
the following areas by playing an important role there:
l Network Design and Communication: Optimal placement of
non-interfering nodes in a network to avoid conflicts and enhance performance.
l Scheduling Non-Conflict Scheduling: Finding and assigning tasks in
large, hierarchical systems where dependencies exist to maximize parallel task
execution.
l Resource Distribution: Resource distribution without overlap becomes
much important in systems where the dependency structure can be graphed in a
tree-like fashion, hence is more linear, or natural, than in the case of more
complicated dependency structures.
l Optimal Sensor Placement within Networks: In tree-structured
networks of sensors, maximizing the set of non-interfering sensors maximizes
coverage and minimizes overlap.
Let's now take a closer look
at one of these applications to see how Largest Independent Set may morph into
useful solutions in the design of networks.
Application in Network Design: Maximizing Non-Interfering
Node Placement
Consider that you are tasked
with designing an efficient wireless communication network. Each node of the
network represents a communication device-a router, cell tower, or sensor. The
network is a tree. Every node communicates with its direct neighbors. In
certain circumstances, the interference coming from the neighboring nodes
causes degradation in both signal quality and the general efficiency of the
network. Your goal is to maximize the number of active nodes, subject to no
more than two of the nearest neighbors being active for any node.
This is the Largest
Independent Set problem.
Representation of the
problem: The network given is in the form of a tree. We have to choose the
largest subset of nodes such that no two nodes in the set interfere with each
other-that is, they are not adjacent. It is exactly this which the LIS
algorithm solves.
This problem can be solved
efficiently using dynamic programming even for large networks. We explore each
node and its children. For every node, you have two options: either include the
node in the independent set and exclude all its neighboring nodes that are
children of it, or exclude the node and include all its children.
We are able to ensure that
the solution obtained is not only optimal but also computationally feasible for
networks with thousands of nodes by calculating the possible independent sets
at each node and storing the result for reuse or by memoization.
Why It Matters: Real-world networks suffer from significant degradation in communication
efficiency due to interference. Solving the LIS problem makes sure that at any
given time, the maximum number of non-interfering communication nodes can be
active; and that would also mean better signal quality, less congestion, and
optimized usage of their resources. Be it for designing a cellular network,
optimizing Wi-Fi routers in an industrial building, or maybe the management of
communication in sensor networks, being able to solve this problem very
efficiently can make a sizeable performance difference.
Conclusion
We have thus unfolded how
some algorithmic thinking combined with dynamic programming and recursion can
solve the Largest Independent Set problem so effi- ciently in a tree. We
started off by understanding what independent sets are, why they are relevant
in the context of trees, and how they provide a basis for solving so many
real-world optimization problems. Dynamic programming through breaking down the
problem into subproblems, and memoization techniques, helped us break through
to an efficient pathway to solving even large trees.
In practice, this LIS
problem appears in network design, resource allocation, task scheduling, and
sensor placement, all of which are domains requiring choices that do not
overlap or conflict with each other. We especially saw how the problem
optimized the placement of communication nodes in tree-structured networks to
achieve maximum signal quality with minimal interference.
Ultimately, the solution to
the Largest Independent Set problem lets us have this rather elegant theory as
well as a powerful practical tool to choose opportunities in anything from
designing networks to managing resources. End Now that you're equipped with
those insights, you're ready to interact with this great algorithm and to apply
it to real-world problems.


Very Informative.
ReplyDeletegreat research & analysis
ReplyDelete